Overview
[Last updated on Feb 2019] Secure file transfers typically employ public key cryptography. This cryptographic system involves the use of two different keys: a public key and a private key. In JSCAPE MFT Server, such keys can be easily generated, imported, and exported in the Key Manager. But some first-time users find it hard to even start using the Key Manager. One reason for that is because they fail to see the difference between server keys and client keys.
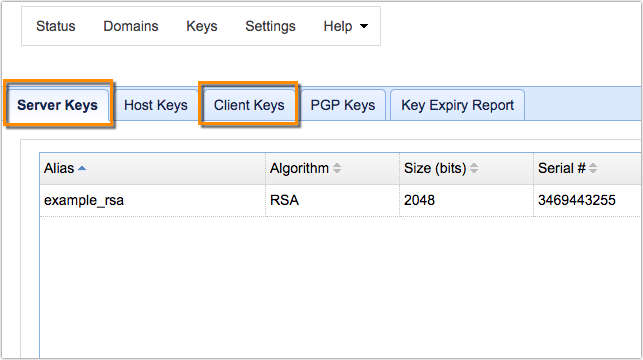
You see, both of them deal with public keys and private keys. Also, whether you generate server keys or client keys, the user interface and the fields you're asked to complete are quite identical.
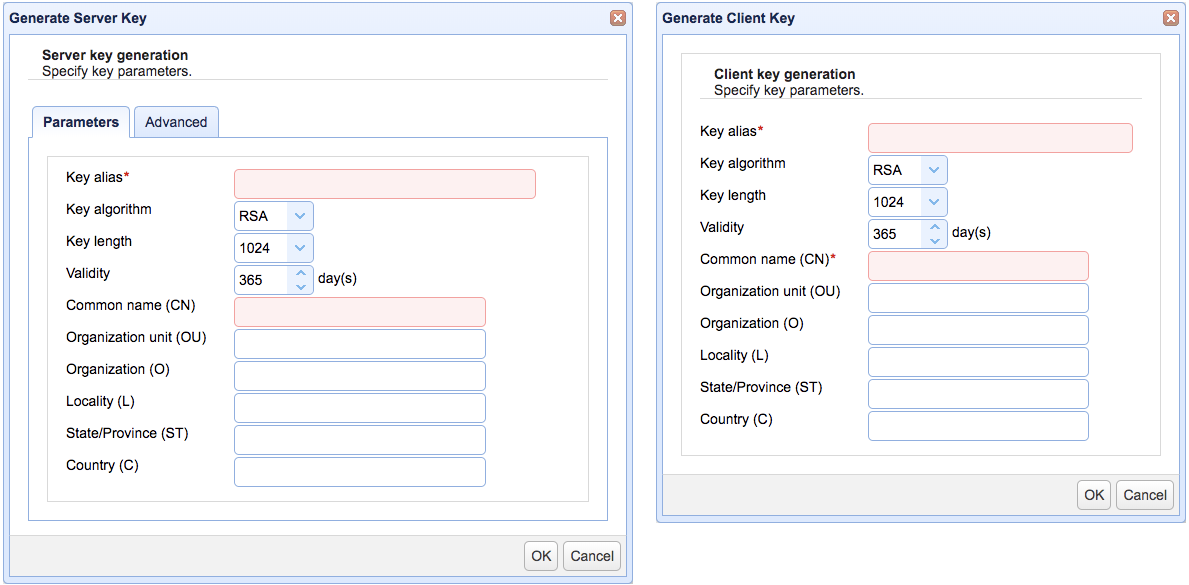
So what exactly is the difference between these two?
Actually, server keys are primarily used for preserving the confidentiality of information contained in your file transfers and for authenticating a server's identity, while client keys are used for authenticating a client's identity.
Perhaps we should start by defining what authentication and confidentiality exactly are.
Authentication and Confidentiality
Authentication and confidentiality are both vital ingredients for achieving information security; in our case, the security of our file transfers. But they're two different things.
Authentication
Authentication allows you to verify the identity of anyone or even anything (as in the case of servers, workstations, and other machines) trying to gain access to your system. For instance, let's say you only want your trusted assistant, George, to download files from a certain directory in your managed file transfer server.
If someone logs in to that directory as George, you would want to make sure that guy is really George and not someone just trying to impersonate him. The most common way of applying authentication is by requiring the person to login using George's username and password. This is known as password authentication. Ideally, George's username and password are things only George would know.
Another way to authenticate a user would be to require the user to submit something that only he should have. One example of this "something" is a private key, which is used in public key authentication. This is what we're interested in here.
Here's a file transfer client (AnyClient) requiring both password authentication and public key authentication:
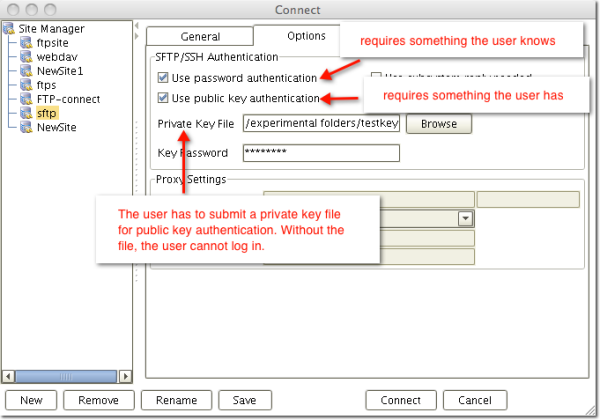
Once you are able to authenticate the identity of a person or machine, you would then be able to enforce other vital elements of information security such as authorization, accountability, and non-repudiation. But these terms are for another post. The next term we would like to define now is "confidentiality".
Confidentiality
Authentication is usually applied at the start of a secure file transfer. Once identities have been verified, file transfers can be allowed to proceed. The next security objective would then be to preserve the confidentiality of whatever information is being transferred. That is, to keep the information private between the sender and the recipient.
In most IT systems, confidentiality is enforced through encryption. Encryption renders normal text (known as plaintext) into something unreadable (known as ciphertext). This can be very useful especially if your file transfers go through highly unprotected networks like the Internet. Once the ciphertext reaches its intended recipient, it can then be transformed back to plaintext by 'decrypting' it.
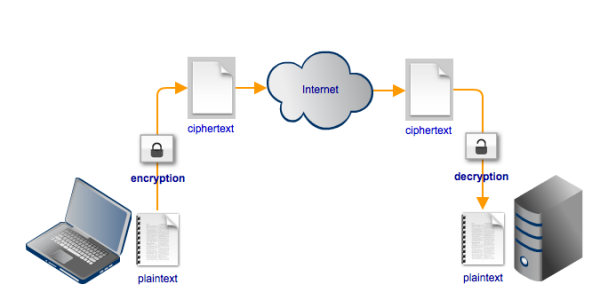
Encryption and decryption are usually done through the use of keys. Some cryptographic systems use just one key for both encryption and decryption. Other systems use two; one key for encrypting and another key for decrypting.
The most widely accepted kind of strong encryption is public key encryption and it uses two keys - a private key and a public key.
How public key cryptography implements authentication and confidentiality
Having learned about authentication and confidentiality, you're probably now in the position to understand how JSCAPE MFT Server uses public key cryptography (a.k.a. asymmetric key cryptography) to implement these two important elements of information security. Let's start by discussing how public key cryptography is able to uphold file transfer confidentiality.
Public keys and private keys for encryption
Public key cryptography makes use of a pair of keys. One key in the key pair is called a private key, while the other one is called a public key. Public keys are used for encrypting files, while private keys are used for decrypting them.
A private key is kept by the key's owner and, as its name implies, is supposed to be kept private. Meaning, only the owner should know what it is or where it is. A public key, on the other hand, is generally shared with others (sometimes, even to the general public).
Proceed to Part 2.